Числата на Фибоначи: математическата последователност, която управлява природата

Числата на Фибоначи представляват една от най-fascinating математическите последователности, която не само очарова математиците с веками, но и се проявява навсякъде в природата около нас. Тази удивителна редица демонстрира как простото математическо правило може да създаде сложни и красиви модели във физическия свят.

Дефиниция и основни характеристики

Числата на Фибоначи в математиката образуват редица, която се дефинира рекурсивно по следния начин: F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2). Започва се с 0 и 1, а всеки следващ член на редицата се получава като сума на предходните два. Първите няколко числа на Фибоначи са 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…

Тази последователност носи името на Леонардо Фибоначи, италиански математик от XIII век, който я представя в своята книга „Liber Abaci“ през 1202 година. Въпреки че редицата е била известна на индийските математици столетия по-рано, Фибоначи е първият, който я популяризира в Западна Европа.

Математически свойства и формули

Ето някои от основните свойства на числата на Фибоначи: НОД(F(n), F(m)) = F(НОД(m,n)) – това означава, че най-големият общ делител на числата F(n) и F(m) е число на Фибоначи с индекс НОД(m,n). Друго важно свойство е формулата F(n+k) = F(k-1) × F(n) + F(k) × F(n+1) за произволно n и k.

Числата на Фибоначи притежават и други забележителни математически свойства. Сумата на първите n числа на Фибоначи е равна на F(n+2) – 1. Всяко трето число на Фибоначи е четно, всяко четвърто е кратно на 3, всяко пето е кратно на 5 и така нататък.

Числата на Фибоначи могат да се бележат и с u(n) в някои математически текстове. Тази алтернативна нотация се използва особено в европейската математическа литература.

Връзка със златното сечение

Една от най-поразителните особености на числата на Фибоначи е тяхната тясна връзка със златното сечение (φ = 1.618…). Когато разделим всяко число на Фибоначи на предходното, отношението се приближава към златното сечение. Колкото по-големи са числата, толкова по-точно е това приближение.

Тази връзка води до формулата на Бине: F(n) = (φ^n – ψ^n) / √5, където ψ = (1-√5)/2. Тази формула позволява директното изчисляване на всяко число на Фибоначи, без да е необходимо да се изчисляват всички предходни числа.

Проявления в природата

Числата на Фибоначи се проявяват изключително често в природните структури. Спиралите на охлювните черупки следват модел, базиран на тези числа. Семената в слънчогледовите корони са подредени в спирали, чийто брой са числа на Фибоначи – обикновено 21 и 34, или 34 и 55.

Листата на растенията често са разположени според числата на Фибоначи. Това явление се нарича филотаксис и гарантира оптимално разпределение на светлината и дъжда. Шишарките на боровете също демонстрират тези числа в спиралите на своите люспи.

Дори човешкото тяло показва връзки с числата на Фибоначи. Имаме 5 пръста на всяка ръка, всеки пръст има 3 фаланги (освен палеца, който има 2), а общо имаме 8 пръста и 2 палеца.

Приложения в изкуството и архитектурата

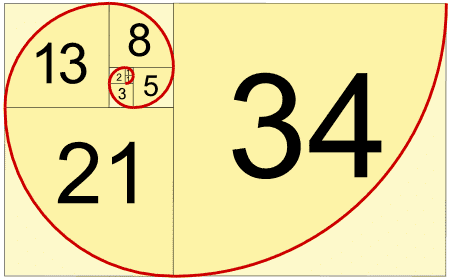
Художниците и архитектите са използвали числата на Фибоначи за създаване на естетически привлекателни творби. Златният правоъгълник, чиито страни са в отношение на златното сечение, може да бъде разделен на квадрати със страни, равни на числа на Фибоначи.

Спиралата на Фибоначи, получена чрез свързване на противоположните ъгли на тези квадрати, се среща в много произведения на изкуството. Тя се използва в композицията на картини, фотографии и дизайна на логотипа на компании.

Алгоритми и изчисления

Изчисляването на числата на Фибоначи е основна задача в програмирането и алгоритмиката. Простата рекурсивна реализация е неефективна за големи числа поради повторното изчисляване на същите стойности. По-ефективни подходи включват динамичното програмиране и матричното умножение.

За много големи числа на Фибоначи се използват специализирани алгоритми, базирани на бързото матрично умножение. Тези методи позволяват изчисляването на F(n) за n с милиони цифри.

Съвременни приложения

В съвременната наука и технологии числата на Фибоначи намират приложение в много области. В компютърните науки те се използват в алгоритмите за търсене и сортиране. Фибоначиевата пирамида е структура от данни, която използва тези числа за оптимизиране на операциите.

В финансовата математика числата на Фибоначи се използват в техническия анализ на финансовите пазари. Търговците използват нивата на Фибоначи за прогнозиране на движенията на цените на акциите и валутите.

Обобщения и разширения

Математиците са разработили много обобщения на числата на Фибоначи. Последователността на Лукас използва същата рекурентна формула, но започва с различни начални стойности. Трибоначи числата са подобни, но всеки член е сума на предходните три.

Матрицата на Фибоначи и нейните свойства водят до дълбоки връзки с линейната алгебра и теорията на групите. Тези разширения показват богатството на математическите структури, произтичащи от простата рекурентна връзка.

Числата на Фибоначи продължават да вдъхновяват математиците, учените и художниците. Тяхната поява в природата демонстрира фундаменталната връзка между математиката и физическия свят. От микроскопичните структури до галактическите спирали, тези числа разкриват универсални принципи на организация и растеж в нашата вселена.